搜索结果: 1-15 共查到“数学 3维ON”相关记录443条 . 查询时间(0.246 秒)
中国科学院物理研究所二维Ruby晶格材料的实现（图）
二维 拓扑 凝聚态物理
2024/9/21
具有非平庸晶格结构的二维材料中存在丰富的物理特性，这些特性由于受到对称性的保护而非常稳定。自以石墨烯和硅稀为代表的蜂窝晶格在布里渊区的K点存在线性色散狄拉克锥特性被发现以来，众多类石墨烯蜂窝晶格的二维晶线图晶格体系由于极有可能是实现拓扑和平带的良好平台而引起了凝聚态物理学的广泛研究兴趣。这些二维线图晶格包括如Kagome晶格、Lieb晶格、Checkerboard晶格、Ruby晶格等。迄今为止，K...
上海微系统所在二维拓扑材料研究领域取得进展（图）
拓扑材料 电子结构 器件
2024/8/28
拓扑绝缘体的体态绝缘，但在其表面或边界处的电子态可形成无耗散的导电通道，在低功耗电子器件具有极大的潜在应用价值而广受关注。例如在二维拓扑绝缘体中，其受保护的拓扑边缘态将在边界处形成一维的自旋极化电子通道，从而实现量子自旋霍尔效应。中国科学院上海微系统与信息技术研究所原位电子结构课题组与中国科学院上海高等研究院、上海科技大学展开联合研究，通过分子束外延法首次成功合成了高质量的二维拓扑绝缘体——蜂窝状...
中国科学院物理研究所二维外尔半金属的实验发现（图）
金属 电子 拓扑
2024/8/21
外尔半金属材料拥有线性色散的外尔锥和独特的手性电子，能够表现出如反常霍尔效应、拓扑费米弧、手性异常负磁电阻等新奇拓扑物性，在新型的量子器件中具有重要的应用价值。此前，人们在TaAs [Science 2015, 349, 613-617]、WTe2 [Phys. Rev. B 2016, 94, 195134]、 Co3Sn2S2 [Science 2019, 365, 1282-1285]等多种...
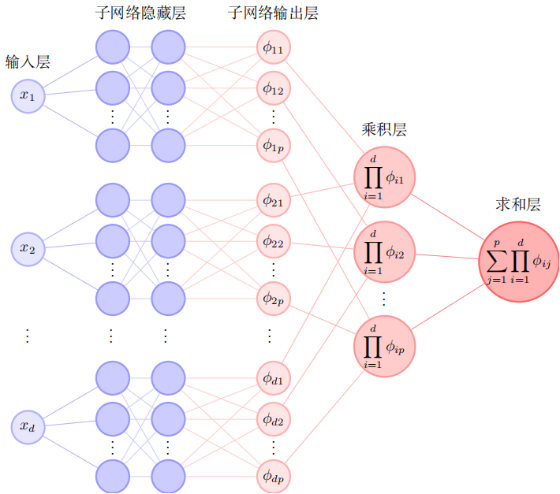
由于“维数灾难”的原因，求解高维偏微分方程一直是数学、物理、化学等学科中具有本质困难的问题。基于深度神经网络的机器学习方法为解决这一问题提供了潜在的可能性，目前已经设计了多种机器学习方法来求解高维偏微分方程。这些方法由于需要进行采样或使用Monte-Carlo方法进行高维积分来计算损失函数，往往导致求解精度远低于经典算法求解低维偏微分方程的精度，实际应用范围也受到了很大的限制。
中国科学院物理所发展出金模板辅助剥离法构筑大面积二维材料及莫尔超晶格
二维材料 莫尔超晶格 拓扑
2024/5/12
莫尔超晶格是由两个或多个单层/少层二维材料以一定的层间转角堆叠在一起而形成的一类新颖的关联电子材料体系。莫尔超晶格体系具有强的电子关联和能带拓扑特性，展现出一系列衍生现象，如非常规超导、莫尔激子、滑移铁电、分数量子反常霍尔效应等。然而，由于传统机械剥离方法获得的单层/少层二维材料的尺寸小且产率低，增加了构筑摩尔超晶格中的角度对准的难度；构筑高质量莫尔超晶格需要避免湿法转移过程，使得近年来发展的金膜...
莫尔超晶格是由两个或多个单层/少层二维材料以一定的层间转角堆叠在一起形成的一类新颖的关联电子材料体系。莫尔超晶格体系具有强的电子关联和能带拓扑特性，展现出一系列的衍生现象，包括非常规超导、莫尔激子、滑移铁电、分数量子反常霍尔效应等。然而由于传统机械剥离方法获得的单层/少层二维材料的尺寸小、产率低，增加了构筑摩尔超晶格中的角度对准的难度；另外构筑高质量莫尔超晶格需要避免湿法转移过程，使得近年来发展的...
中国科学院科学家在二维量子磁体中发现“拓扑克尔效应”（图）
量子磁体 拓扑克尔效应
2024/4/11
2024年4月8日，中国科学院合肥物质科学研究院与中国科学技术大学等合作，依托稳态强磁场实验装置（SHMFF），在二维新型量子磁体斯格明子元激发的理论与实验研究中取得进展，提出“拓扑克尔效应”的概念。
中国科大在二维量子磁体的拓扑元激发研究中观察到新奇“拓扑克尔效应”（图）
二维量子 磁体 拓扑
2024/6/14
2024年4月4日，中国科学技术大学与中国科学院强磁场科学中心、山西师范大学、西安交通大学、河南大学、河南省科学院等单位合作，在二维新型量子磁体斯格明子元激发的理论与实验研究中取得重要进展，提出“拓扑克尔效应（TopologicalKerrEffect, TKE）”的概念。该成果4月4日以“Topological Kerr effects in two-dimensional magnets wi...
一类二维双曲混沌偏微分系统的可观性与观测器
二维双曲混沌 偏微分系统 可观性 观测器
2023/12/13
This paper is concerned with both observability and observers for a class of systems described by the two-dimensional hyperbolic PDEs with superlinear boundary conditions which can exhibit chaos. The ...
In this paper, we prove that the \(L^p(\mathbb {R}^d)\) norm of the maximal truncated Riesz transform in terms of the \(L^p(\mathbb {R}^d)\) norm of Riesz transform is dimension-free for any \(2\le p<...
Academy of Mathematics and Systems Science, CAS Colloquia & Seminars：基于stPCA降维算法的ICU病人出院策略法
stPCA降维算法 ICU病人 出院策略法
2023/12/11
许多复杂生物系统可以由高维非线性动力系统描述，对原始数据进行降维有助于对这些系统进行有效分析。然而以一种可解释的方式进行极致低尺度的降维仍然是一个具有挑战性的问题。基于Takens延迟嵌入理论，将高维空间信息转换为低维时间信息，我们开发了极致低降维算法stPCA，并将其应用于重症监护医疗信息管理系统MIMIC-III和MIMIC-IV数据集，提出了ICU病人的出院决策。stPCA基于ICU患者的高...
2023年3月27日，中国科学院南海海洋研究所热带海洋环境国家重点实验室（LTO）谢培炜博士构建了基于纳维-斯托克斯求解器的强非线性海啸波浪生成模型。该模型的构建弥补了海啸灾害领域中强非线性波浪生成模型的缺失，并在国际范围内首次实现对典型海啸波浪记录的模拟重现。相关成果由谢培炜博士为第一作者，杜岩研究员为共同作者，发表在国际期刊Coastal Engineering上。
In this paper, we consider boundary output regulation for one-dimensional reaction–diffusion equation that has disturbances entering the system from in-domain and both boundaries. The reference signal...
差异性的统计推断方法及其应用（张维、李启寨）
差异性 统计推断方法 应用
2023/2/22
差异性分析是生物医学研究中的一个重要问题。它旨在通过比较两组或多组样本数据之间的差异来识别影响复杂疾病或性状的基因、生物通路、微生物等。针对人类微生物组和水稻耐寒性的差异性分析问题，提出了自适应的分组聚合检验方法，给出了统计显著性的快速算法及其统计性质，利用多尺度分析方法有效地整合水稻耐寒性的两个性状，提出了群体分层校正方法并将其应用到水稻耐寒性的数据中，发现并验证了与水稻耐寒性相关联的基因COL...
对于高维带粘性的标量守恒律方程和可压缩Naiver-Stokes方程，证明了平面粘性激波和疏散波在高维周期扰动下的非线性渐近稳定性。证明的关键在于如何构造合适的拟设来抵消在无穷远处持续振荡的周期扰动，从而可以建立能量估计。特别地，在激波稳定性的结果中，文章给出把扰动的零频和非零频分开估计、再结合反导数技巧的新想法，使得基本能量方法可以得到利用，同时还揭示了周期振荡对激波稳定性的影响与非振荡扰动有本...